2.5.
Rectas de colores.
a)
Con la ventana
algebraica a la vista Escribe en la barra de entrada
m=2, después
n=3. Pulsa sobre el círculo
blanco de m y n que hay junto a las variables de la vista algebraica
para que aparezcan como deslizadores en la ventana gráfica. Es
conveniente que tengamos a la vista su nombre y valor (en
Propiedades/Básico).
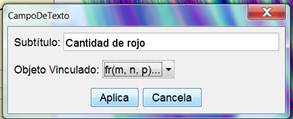
b)
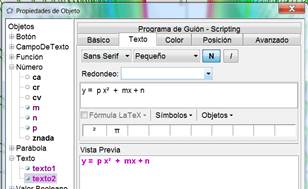
En la barra de
entrada escribimos y = m*x+n
(también es válido y=m x+n,
con espacio entre m y x)
c)
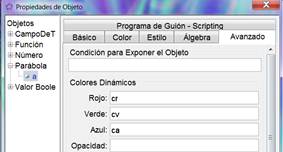
Con botón derecho
sobre la recta (o sobre su ecuación), vamos a Propiedades/Avanzado,
colocamos en Color dinámico fórmulas en los colores Rojo, Verde y Azul.
Haremos que esas fórmulas dependan de
m y
n para que cambien el color
cuando realicemos la animación de los deslizadores.
d)
Hacemos además que la
recta deje rastro a su paso. Aquí tenemos algunos ejemplos.
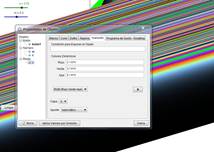
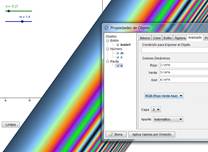
e)
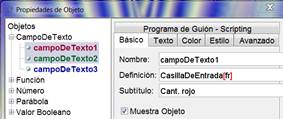
Colocamos un botón de
“limpieza de rastros” (idéntico al que hicimos para el apartado 5c) para
que cada vez que lo pulsemos haga el efecto de hacer un zoom que no
llega a alejar la imagen pero hace una Actualización de la ventana
gráfica con lo que limpiará los rastros que ha dejado nuestra recta.
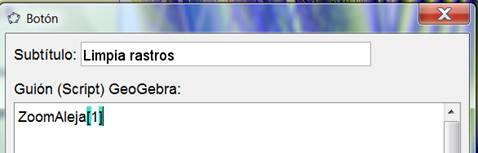
f)
Fase de presentación:
Fijar los elementos (textos, casillas de control y deslizadores) para
que no se muevan al pulsarlos.
g)
Concurso: Es la
última fase. Cada alumno experimenta con diversas funciones en los
colores dinámicos. Cuando encuentra un diseño que le gusta, selecciona
la zona de la parte gráfica que más le agrada para copiarla en un
documento de Word. En la parte inferior debe colocar una leyenda que
indique el autor, la/s variable/s que han tenido animación y las
fórmulas introducidas en los tres colores. La siguiente imagen es la de
la ganadora del concurso celebrado en 4º A del IES Sant Blai de Alicante
durante el curso 2011-12 en
la sección “animación de la ordenada en el origen”:

Autora: Paula López
Animación n
Rojo 2/(m + n)
Verde 3/ (m + n)
Azul 4/ (m + n)
Archivo
12_rectas_col.ggb