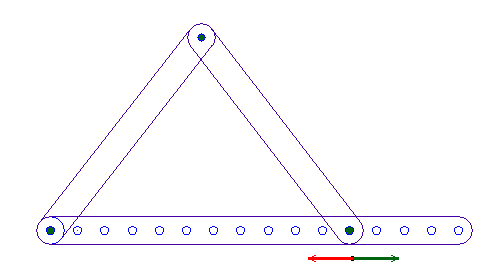
El gato elevador está formado por tres barras articuladas que forman un triángulo, en el que la base es de longitud variable y los otros dos lados tienen longitud fija. Cuando alargamos o acortamos la base, hacemos que el tercer vértice se sitúe a distintas alturas:

Las construcciones geométricas admiten multitud de enfoques y grados de aproximación y profundización. Queremos montar un triángulo articulado con dos varillas de longitud fija y una tercera que se pueda alargar o acortar. Si utilizamos tiras de cartulina, nuestra preocupación será estudiar la forma de hacer las uniones o la forma de conseguir una varilla extensible.

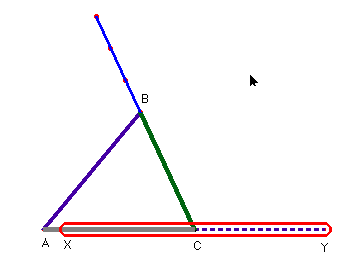
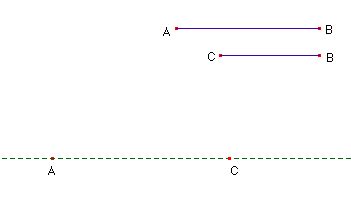
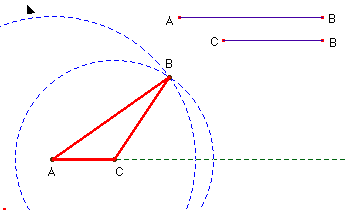
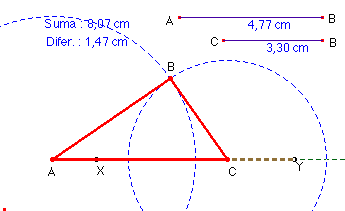
Cuando la herramienta es un programa de ordenador que utiliza puntos, segmentos, polígonos, etc., hay que revisar las relaciones entre los objetos que se relacionan en el sistema para captar los elementos básicos que lo hacen funcionar. El triángulo puede ser visto desde los vértices: uno de ellos es fijo, otro se desplaza por un segmento y el tercero vendrá determinado por los dos segmentos de longitud definida de antemano, es decir, será el punto de intersección de dos circunferencias.

Para una primera aproximación es conveniente que dibujemos previamente las dos varillas de longitud fija AB y BC , un punto A que será fijo y otro C que se puede desplazar –en principio -, sobre una recta que pasa por A.

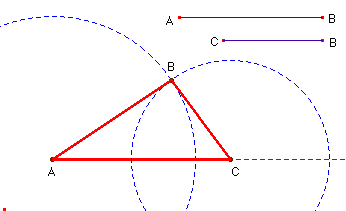
Para obtener la posición del tercer vértice, podemos trazar una circunfe-rencia con radio igual al segmento AB y centro en A. Igualmente, se traza la circunferencia de radio CB con centro en C. El punto B será cualquiera de los dos puntos de intersección de estas circunferencias. Podemos desplazar C a lo largo de la semirecta para obtener los posibles triángulos

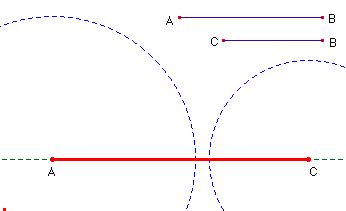
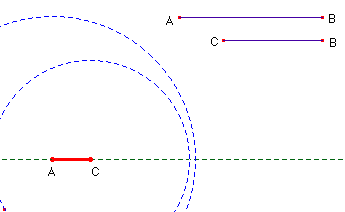
Para investigar la construcción: modificamos las longitudes de los seg-mentos o la posición de algunos de los puntos que le han servido de base. Aquí empiezan los problemas, porque nos encontraremos con situaciones en las que el triángulo no existe, el motivo es que las circunferencias no tienen intersección.

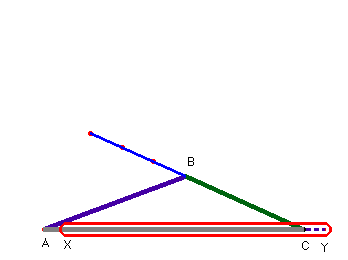
Nos replantearnos la situación para estudiar el conjunto de posiciones sobre las que se puede mover C, para que el triángulo pueda ser construido, es decir, cuando AC está entre AB-BC y AB+BC. Obtenemos dos puntos: X e Y que serán los extremos del segmento sobre el que queremos que se desplace libremente C. Ahora no tenemos más que redefinir el punto C para que, en lugar de pertenecer a la semirecta, esté situado únicamente sobre el segmento XY.

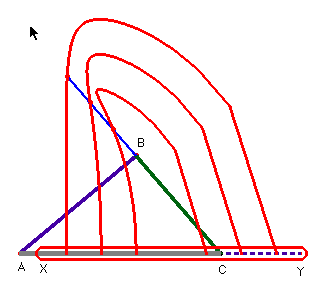
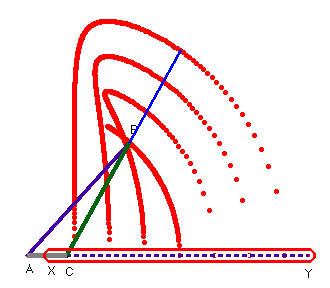
Como se ha visto anteriormente, en el gato elevador los desplazamientos horizontales del punto C consiguen que B se sitúe a diferentes alturas. Es más, podemos alargar el segmento BC, y situar sobre él diferentes puntos de apoyo para estudiar las distintas trayectorias que siguen esos puntos cuando C se desplaza sobre el segmento. En el dibujo de la parte superior se ha dejado la traza activada de los cuatro puntos marcados sobre el segmento, para analizar los distintos caminos que seguirán. Otra forma de hacerlo sería con la herramienta Lugar Geométrico –el dibujo inferior-, que es especialmente interesante porque los lugares geométricos se transforman automáticamente cuando modificamos las longitudes iniciales de los segmentos, algo que no ocurre con el rastro que deja la traza cuando está activada.