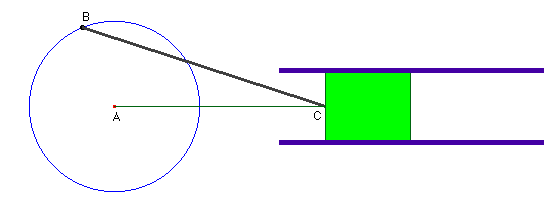
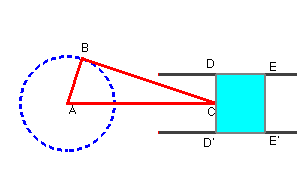
Uno de los ejemplos tradicionales de la relación entre el movimiento de rotación con el desplazamiento en vaivén lo constituye el funcionamiento de la máquina de vapor. Aquí tenemos un triángulo de base variable. El punto impulsor es C, está sujeto a un émbolo que está sujeto a un movimiento de vaivén en el interior de un cilindro y se traduce en un movimiento de rotación de B alrededor de A para mover una rueda.

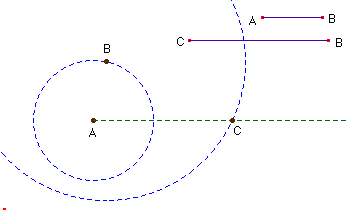
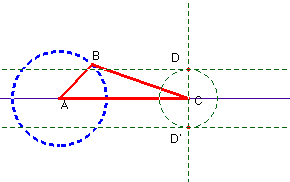
Para analizar el modelo de la máquina de vapor, en lugar de situar el punto C sobre un segmento XY, como en la construcción del gato elevador, hacemos que el grado de libertad del sistema recaiga sobre el punto B. La condición que debemos imponer a este punto es distinta a la construcción del gato. Como el segmento AB tiene longitud fija, B ha de ser un punto situado sobre la circunferencia de centro A y radio AB. Para situar la otra varilla de longitud fija debemos hacer una nueva circunferencia de centro B y radio BC, de esta ma-nera tendremos una circunferencia que corta a la semirecta en el punto C.

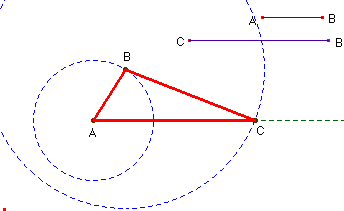
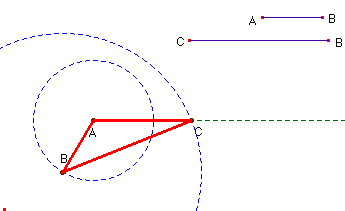
El triángulo de base variable tendrá ahora otra apariencia; un punto B gira alrededor de A e impulsa una biela, uno de cuyos extremos es obligado a moverse por una línea recta.

El punto C es el que debe arrastrar consigo el rectángulo que simula el pistón. Uno de los lados del triángulo estará situado sobre la recta perpendicular al segmento AC que pasa por C, tomamos dos puntos de esa recta D y D’ que estén a la misma distancia de C que serán dos vértices.

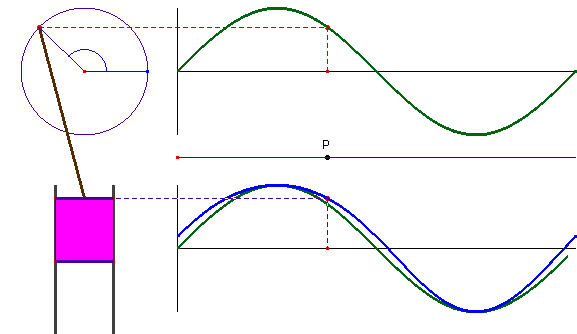
El diseño de la máquina de vapor es útil para profundizar en conceptos matemáticos, como la medida de ángulos y las funciones trigonométricas. Con un punto, que gira alrededor de una circunferencia de radio unidad, es sencillo dibujar la función seno como la medida de la distancia del punto al eje de abscisas.

Podemos utilizar el sistema biela-manivela de la construcción del motor de explosión para estudiar la altura que alcanza el émbolo en el cilindro, y construir la gráfica que determina la posición de este punto cuando da una vuelta completa. Es interesante comparar esta gráfica con la función seno, veremos que hay pequeñas diferencias, algunas de ellas vienen marcadas por detalles que no son fáciles de detectar: en la construcción vemos que tarda más en ir de derecha a izquierda por la parte de arriba que al revés, consecuencia de esto es que la gráfica que indica la posición del cilindro –en azul- esté por encima de la del seno, excepto en dos puntos: ?/2 y 3?/2 que son los únicos en los que ambas coinciden.