|
Otro enfoque del trabajo puede venir de la búsqueda de nuevos polígonos dentro del cuadrado, han aparecido rectángulos triángulos de varios tipos, trapecios, polígonos de muchos lados. Hay otros polígonos conocidos que aún no han aparecido. La propuesta de trabajo puede animar a considerar polígonos de distinto número de lados, a que consigan polígonos cóncavos. También podemos proponer figuras conocidas que puede que no hayan aparecido hasta ahora como el rombo, el trapecio isósceles, el paralelogramo, el pentágono o el hexágono. La pregunta podría ser: ¿Qué otros polígonos conocidos podríamos encontrar en el interior del cuadrado cuya área sea la mitad? Los alumnos encuentran trapecios isósceles cuando la suma de las bases es igual al lado del cuadrado y también paralelogramos que tienen por base la mitad del lado y por altura el lado del cuadrado, y no es necesario que utilicen los vértices del cuadrado.
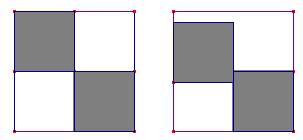
Paralelogramo Trapecio isósceles La idea de utilizar desplazamientos da sus frutos al revisar el trabajo realizado y obtener polígonos convexos (octógono) donde antes obteníamos polígonos cruzados y en algunos caso eran rechazados como polígonos. Desplazamiento de regiones En el trabajo previo seguramente han aparecido pentágonos y otros de mayor cantidad de lados. Es más fácil que encuentren los convexos que los cóncavos. A partir del procedimiento consistente en tomar los puntos medios de los cuatro lados y obtener un nuevo cuadrado, algunos alumnos se dan cuenta de que pueden quitar restricciones a los puntos, que dos estén en los puntos medios y los otros no, y otros casos que podemos ver en esta imagenLos cuadrados se convierten en cometas, trapecios paralelogramos y otros cuadriláteros:
Cometa Trap isósceles Cuadrilátero 1 Paralelogramo Los cuadrados se han transformado en cometas, trapecios paralelogramos y otros cuadriláteros:
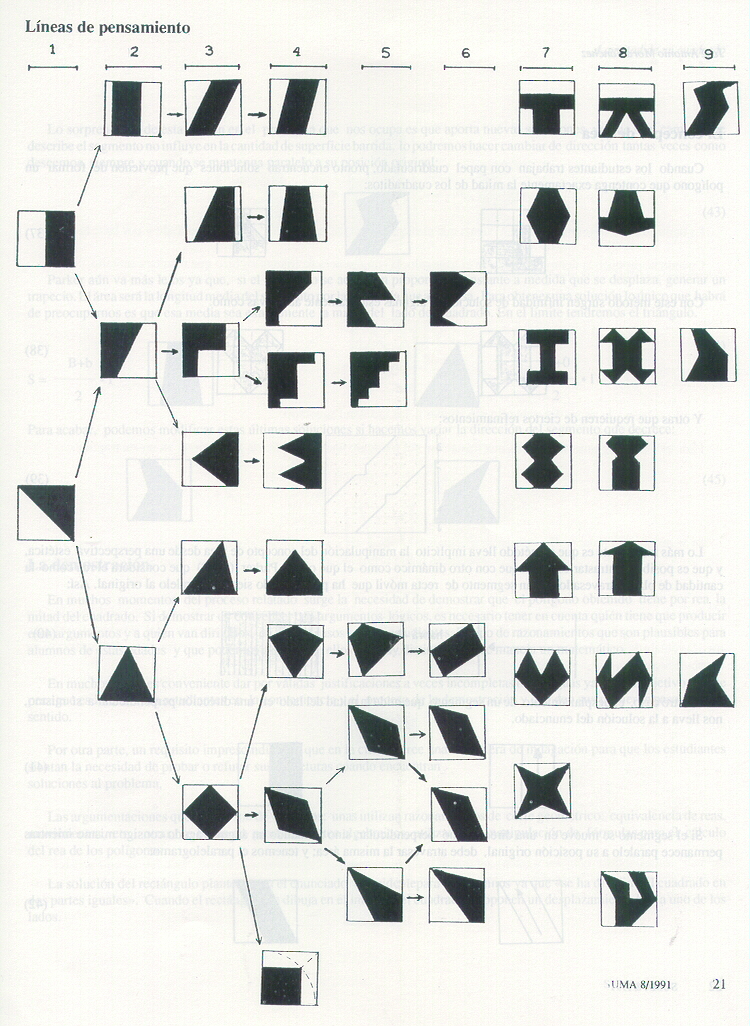
Cuadrilátero 2 Cometa Paralelogramo Cuadrilátero 3 En el artículo de 1991 compuse un diagrama que, con el título "líneas de pensamiento", intentaba reflejar cómo aparecían unas soluciones a partir de otras ya conseguidas:
|
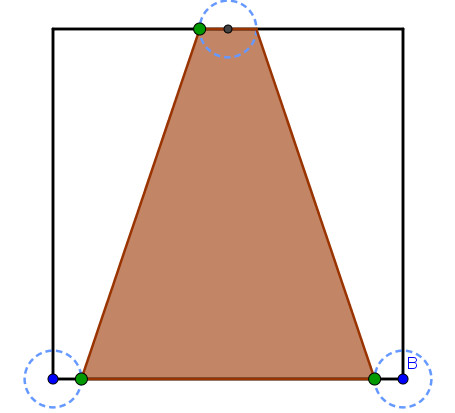
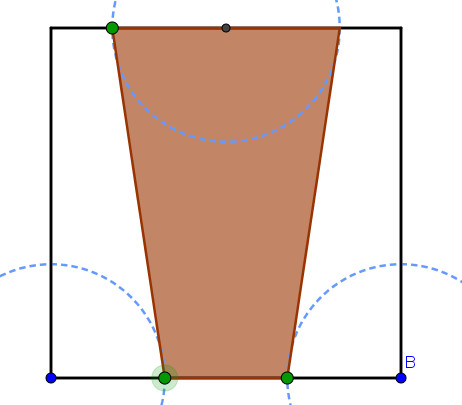
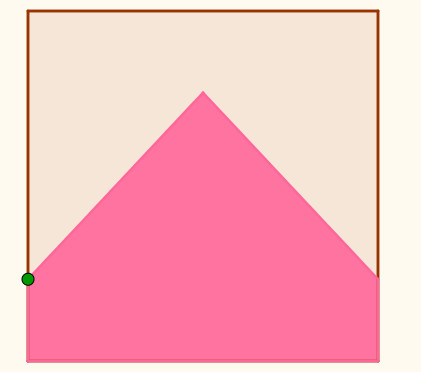
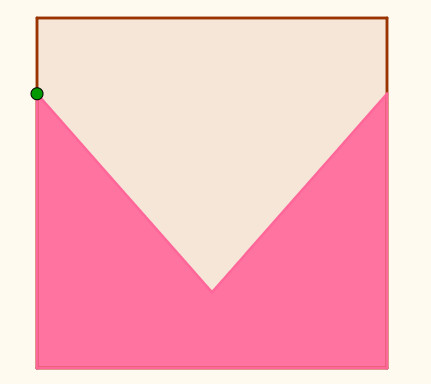
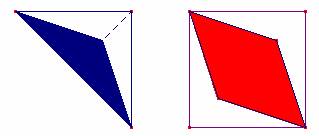El rombo es una de las soluciones que
cuesta aparecer. No es fácil encontrar los dos vértices que no
están en las diagonales. Cuando se consigue, esta solución
admite generalizaciones a figuras que tengan sus vértices en dos
paralelas a la diagonal del cuadrado que pasan por los puntos
medios de los lados. Obtenemos dos cometas, un paralelogramo y
un cuadrilátero.
