|
En muchos momentos del proceso relatado surge la necesidad de demostrar que el polígono obtenido tiene por área la mitad del cuadrado. En secundaria podríamos convenir que demostrar es convencer con argumentos lógicos, pero hay que tener en cuenta quién tiene que producir esos argumentos (los estudiantes) y a quién van dirigidos (sus compañeros). El tipo de argumentos que son esperables en estas edades es distinto del que maneja el matemático.
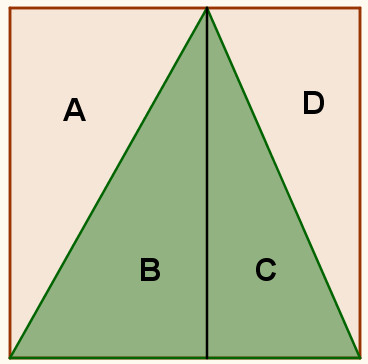
En muchos casos es conveniente dar por válidas justificaciones a veces incompletas o ambiguas ya que el objetivo que se persigue es iniciar a los estudiantes en la conveniencia de demostrar y en el proceso de demostración y que den sus primeros pasos en este sentido. Como se ha señalado al principio, es fundamental que se cree en clase una atmósfera de indagación para que los estudiantes sientan la necesidad de probar o refutar sus conjeturas cuando encuentran soluciones al problema. Los argumentos más frecuentes son de tipo geométrico: equivalencia de áreas, movimientos en el plano, etc. Mas difícil es que surjan de los alumnos los procedimientos algebraicos como la manipulación de fórmulas para el cálculo del área de los polígonos. La primera solución del rectángulo resulta evidente para los alumnos ya que se ha dividido el cuadrado en dos partes iguales, cuando el rectángulo se dibuja en el interior del cuadrado, proponen un desplazamiento hacia uno de los lados. El profesor puede sugerir la obtención del área mediante la fórmula para el rectángulo. Cuando se les propone la demostración para el triángulo, suelen utilizar la congruencia de triángulos: A=B y C=D
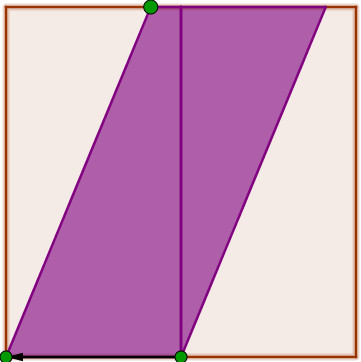
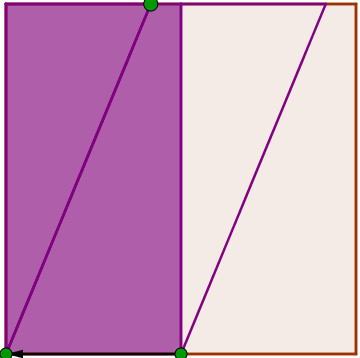
También aquí el profesor puede proponer la utilización de base por altura dividido por dos. En el paralelogramo, se ve que una traslación del triángulo hacia la izquierda, lo convierte en un triángulo. En cambio, para el trapecio los alumnos propusieron realizar un giro de 180º alrededor del centro del cuadrado para superponer los dos trapecios. La demostración algebraica, que toma en cuenta que la suma de las bases es igual al lado del cuadrado, tuvo la ventaja de ser útil para otros tipos de trapecios.
La demostración del giro se mantuvo disponible cuando se toman líneas con centro de rotación de orden 2.
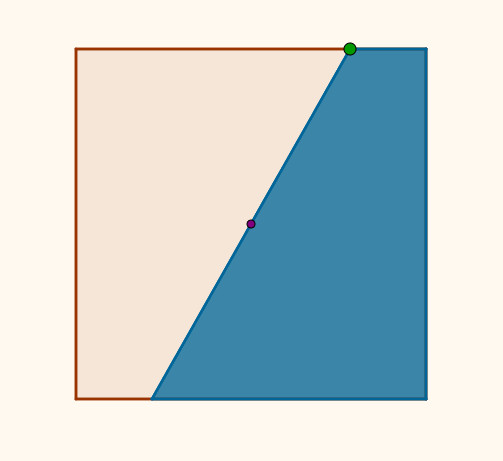
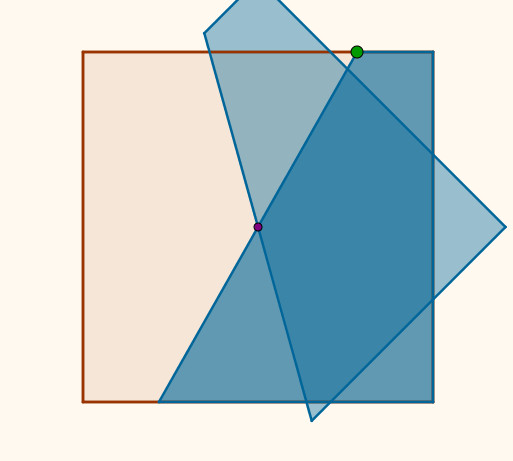
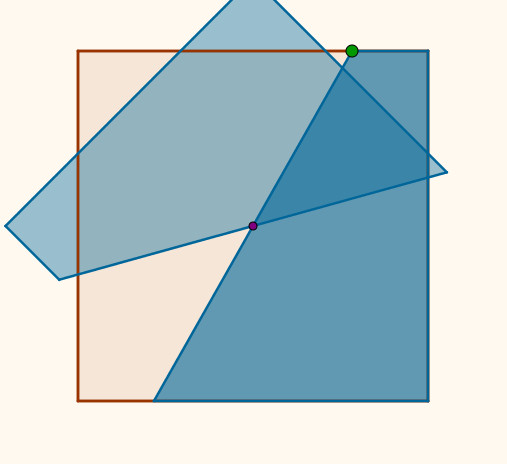
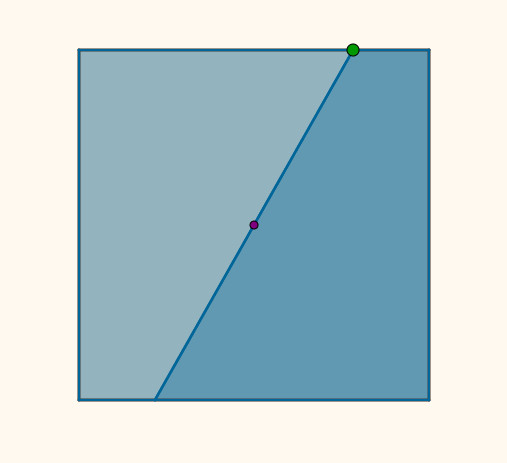
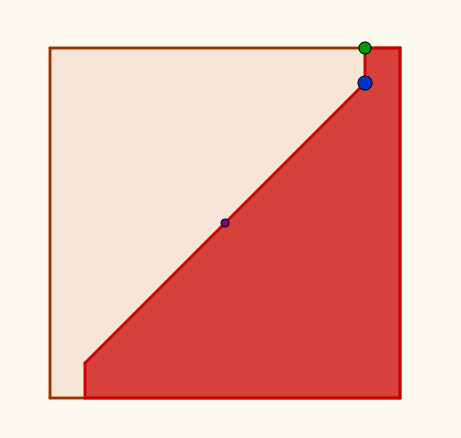
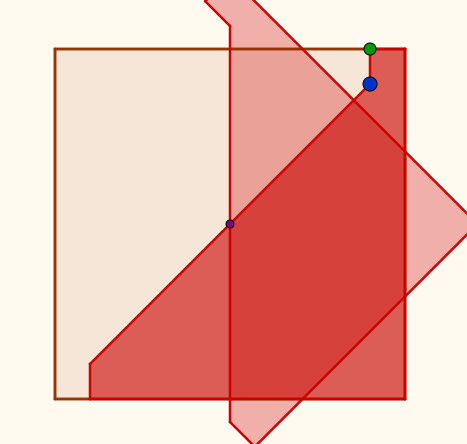
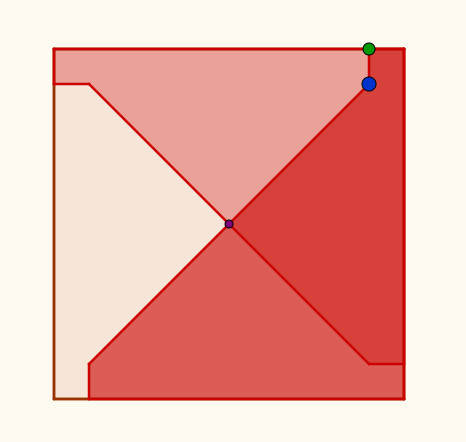
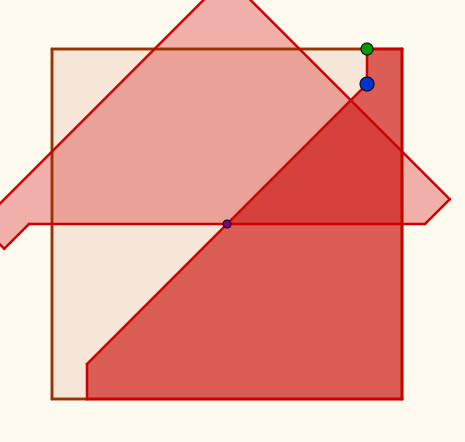
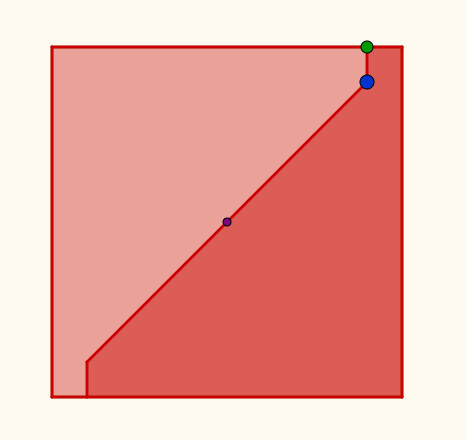
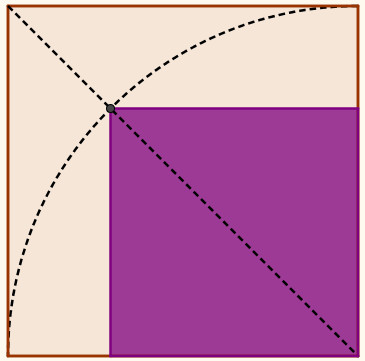
Avanzado el trabajo, se les propuso demostrar que, según se hace la construcción del cuadrado coloreado de la figura de abajo, su área será la mitad del grande.
|