|
Podemos llevar la mitad del cuadrado a
cursos posteriores en los que queramos introducir a los
estudiantes en la idea del infinito y hacer aflorar una paradoja
clásica que se deriva de un abusivo paso al límite. Las
siguientes construcciones son soluciones de la mitad del
cuadrado:
.jpg) .jpg) .jpg) .jpg) .jpg) .jpg)
La sucesión de los perímetros de las
mitades sombreadas es una sucesión
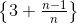 que tiende a 4, pero en el límite, la línea poligonal tiende a
la diagonal, es decir, en el límite debería valer . La cuestión
la reconoció Rafael Losada del IES Pravia de Asturias como una
falsa paradoja, porque las poligonales no corresponden a
funciones derivables, por lo que no se puede asegurar que la
sucesión de las longitudes converja a la longitud del límite.
que tiende a 4, pero en el límite, la línea poligonal tiende a
la diagonal, es decir, en el límite debería valer . La cuestión
la reconoció Rafael Losada del IES Pravia de Asturias como una
falsa paradoja, porque las poligonales no corresponden a
funciones derivables, por lo que no se puede asegurar que la
sucesión de las longitudes converja a la longitud del límite.
Otra forma de acercarnos al concepto de
infinito es mediante una suma infinita de fracciones:
.jpg)
Se trata de
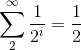 ,
es decir: ,
es decir:
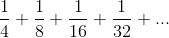 Se
utiliza un procedimiento en el que cada cuadrado nuevo tiene por
lado Se
utiliza un procedimiento en el que cada cuadrado nuevo tiene por
lado
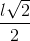 siendo l el lado del anterior y se forman figuras que
después se puedan repetir por autosemejanza.
siendo l el lado del anterior y se forman figuras que
después se puedan repetir por autosemejanza.
Anterior
Índice
Siguiente
|
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
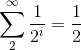 ,
es decir:
,
es decir: