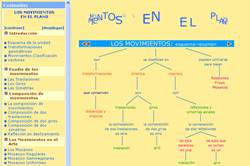
La Geometría de los movimientos … en movimiento.
Publicado en la Sección Nuevas Tecnologías del número 51 de la revista UNO. Abril a Junio de 2009. Páginas 123 a 125.
Las matemáticas de secundaria ponen cada vez más énfasis en una
geometría de propiedades, relaciones, clasificaciones, construcciones y
razonamientos sobre formas y estructuras. Se intenta que el alumno
desarrolle la visión espacial, que comprenda las distintas
representaciones del mundo físico y creen modelos a partir de
situaciones reales.
Para conseguir todo esto es necesario revisar los contenidos
matemáticos. Hay partes del currículo que pierden valor mientras otras
lo aumentan. Por otra parte, necesitamos disponer de herramientas que
permitan un acercamiento que favorezca el aprendizaje. Es la eterna
relación entre el qué y el cómo, entre los contenidos y la metodología y
en geometría es inevitable.
Los dos movimientos del título tienen que ver con las afirmaciones
anteriores. La geometría de las transformaciones aporta una forma de
interpretar e investigar los objetos geométricos y realizar aproximación
al mundo físico y al artístico. Además, el desarrollo de las nuevas
tecnologías, los programas de geometría dinámica e Internet -la
competencia digital-, permiten que ese acercamiento se acompañe de
elementos visuales e interactivos como nunca antes habíamos podido
disponer.
Geometría del movimiento de Teresa Ruiz,
http://www.isftic.mepsyd.es/w3/eos/MaterialesEducativos/mem2003/movimientos/
Presenta los movimientos mediante una colección de pequeñas animaciones
muy atractivas por su sencillez y cuidada presentación. Se detallan las
características principales de cada uno de los movimientos y sus
aplicaciones al estudio de los frisos y mosaicos.
Geometría interactiva aplicada al estudio de los movimientos en el
plano, de María José Sánchez Quevedo
http://concurso.cnice.mec.es/cnice2006/material105/inicio.html
Utiliza animaciones Cabri para realizar una propuesta muy completa del
estudio de los movimientos en el plano para los cursos de 3º y 4º de
ESO. Son muy interesantes las secuencias de generación de varios de los
mosaicos de Escher a partir de figuras poligonales: las transformaciones
de sus lados y la colocación de baldosas.
Geometría dinámica del equipo G4D
La web contiene una amplia colección de actividades realizados con
GeoGebra y Cabri. En
La web de José
http://mimosa.pntic.mec.es/clobo/geoweb/movi.htm
Mosaicos de Ángel Corral Cedena
Un estudio en profundidad de los mosaicos con animaciones realizadas en
Geogebra, Cabri y flash que muestran la construcción detallada paso a
paso de muchos mosaicos islámicos y de Escher que exponen gráficamente
las propiedades geométricas internas.

Simetría de
Secuencia de aprendizaje de la simetría con enlaces a multitud de
recursos externos: applets, geoplanos, rompecabezas, caleidoscopios,
juegos y otras páginas.
Tilings and Tessellations. Geometry Centre.
http://www.scienceu.com/geometry/articles/tiling/index.html
Gran recopilación de recursos en la red para el estudio de los mosaicos.
Incluye un applet de Kaly que permite generar cualquiera de los 17
mosaicos.
Symmetry it’s around you de Adrian Bruce.
http://www.adrianbruce.com/Symmetry/
Puede que sea la web más completa en su intento de mostrar la simetría
(axial y rotacional) y sus manifestaciones a nuestro alrededor: el
rostro humano, los edificios, la naturaleza, las actividades humanas, la
tecnología, los símbolos religiosos. Dispone de interesantes applets
para mostrar los conceptos en movimiento.
Escher in the classroom de Jill Britton.
http://britton.disted.camosun.bc.ca/jbescher.htm
Los trabajos de M.C. Escher
adaptados para incorporarlos a la clase de matemáticas. Contiene muchos
applets que muestran sus técnicas y cómo las podemos aprovechar en
clase. En el siguiente enlace, la autora nos ofrece una amplísima
colección de enlaces de Internet para trabajar la simetría y los
mosaicos.
http://britton.disted.camosun.bc.ca/jbsymteslk.htm
Principles & Standards for School Mathematics del N.C.T.M.
http://standards.nctm.org/document/eexamples/chap6/6.4/index.htm
Actividades interactivas que permiten visualizar las isometrías,
identificar transformaciones ocultas o estudiar la composición de
movimientos.
Software para el estudio de los movimientos en el plano y
la construcción de mosaicos:
Kaleidomania
http://www.keypress.com/x6173.xml
Tesselmania
http://www.tessellations.org/tesselmania0.htm
Tess
http://www.peda.com/download/
Kaleidodraw de Protozone
http://www.protozone.net/kal/KalDemo.html
Kali
http://www.scienceu.com/geometry/handson/kali/kali.html
José Antonio Mora