Pitágoras y sus discípulos utilizaban piedrecillas (en latín calculus) o marcas que disponían según determinadas formas geométricas. De ese modo podían asociar números y formas, cambiar estas y observar lo que ocurría con los respectivos números, relacionar unas formas con otras, unos números con otros, etc. En definitiva, trabajaban con la forma y el número a la vez. Los resultados fueron extraordinarios y permitieron descubrir importantes teoremas y relaciones.

Llamaban triangulares a los números que correspondían a disposiciones de piedrecillas formando triángulos: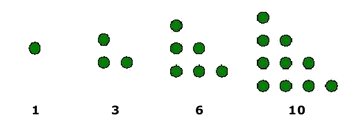

Llamaban cuadrados a aquellos números que se obtenían al distribuir puntos o piedrecillas de modo que la imagen obtenida fuese la de un cuadrado: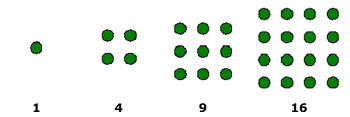

Daban el nombre de rectangulares u oblongos a los números que se obtenían al distribuir las piedrecillas de modo que se obtuviesen determinados rectángulos: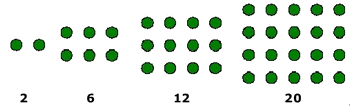

Del mismo modo definían los números pentagonales, hexagonales, octogonales, etc.

A lo largo de la historia ilustres matemáticos como Gauss o Euler también dedicaron su tiempo al estudio de los números poligonales.

Usa la aplicación y responde:

1. Pulsa . Mueve el deslizador inferior y observa la formación de los números rectangulares. Haz clic sobre la casilla Tabla de valores y completa la columna Rectangular de la tabla siguiente:

2. Si tomamos como dimensiones de cada uno de los rectángulos el número de círculos que lo forman, a lo largo y a lo ancho, ¿qué dimensiones tiene el rectángulo que corresponde al número rectangular 1.º? ¿Y el rectángulo del número rectangular 2.º? ¿Y el del 3.º? ¿Y el del 10.º? ¿Y el del número rectangular 100.º? ¿Cómo puedes calcular el número rectangular a partir de las dimensiones del rectángulo correspondiente?

3. ¿Qué dimensiones tendrá el rectángulo que ocupa el lugar n? ¿Qué fórmula podemos utilizar para calcular el número rectangular que ocupa el lugar n? Completa:

R(n) = ........

4. Pulsa  para desactivarlo y pulsa . Mueve el deslizador inferior y observa la formación de los números triangulares. Haz clic sobre la casilla Tabla de valores completa la columna Triangular de la tabla.

5. Compara los números de las dos columnas. ¿Qué relación encuentras?

6. Vamos a buscar una interpretación geométrica a la relación anterior. Pulsa  y  Mueve el deslizador inferior. ¿Se corresponde lo que observas con la relación que has descubierto en la tabla?

7. Teniendo en cuenta la relación anterior, ¿qué fórmula podemos utilizar para calcular el número triangular n? Completa:

T(n) = ........

8. Escribe la diferencia entre cada número triangular y el número triangular siguiente. ¿Qué observas?

9. Calcula la diferencia entre cada número triangular y el que va dos posiciones hacia adelante. ¿Cómo aumentan esas diferencias? ¿Cómo aumentan esas diferencias entre números separados tres posiciones?

10. Otra forma de calcular el número triangular consiste en sumar el número de círculos de cada una de las filas que lo forman. Si observas el número triangular de arriba a abajo, ¿qué suma tendrías que hacer para hallar el número triangular 2? ¿Y el 3? ¿Y el 4? ¿Y el 10? ¿Y el 100?

11. ¿Cómo podemos calcular la suma de los n primeros números naturales? Completa:

1 + 2 + 3 + 4 + 5 + .... + n = ........

10. Pulsa  y . Pulsa ahora el botón . Mueve el deslizador inferior y observa la formación de los números cuadrados. Activa la casilla Tabla de valores y completa la columna Cuadrado de la tabla.

11. Busca una fórmula para obtener el número cuadrado de orden n. Completa:

C(n) = ........

12. ¿Es cierta la relación: R(n) = C(n) + n? Compruébalo en la tabla y también gráficamente. (Activa simultáneamente los botones  y  y trata de interpretar la figura).

13. Pulsa  y . Mueve el deslizador de la parte inferior. Observando las figuras que se van formando, ¿observas alguna relación entre los números cuadrados y los triangulares? Comprueba en la tabla la relación que has encontrado. ¿Cómo la escribirías algebraicamente?

14. Pulsa . Mueve el deslizador inferior y observa la formación de los números pentagonales. Activa la casilla Tabla de valores y completa la columna Pentagonal de la tabla.

15. Comprueba que cada número pentagonal es igual a la suma del número cuadrado del mismo orden y el triangular de un orden inferior. Intenta buscar alguna relación más entre los números pentagonales y los que has obtenido anteriormente.

16. Pulsa . Mueve el deslizador superior y observa la formación de los números hexagonales. Activa la casilla Tabla de valores y completa la columna Hexagonal de la tabla.

17. Trata de encontrar alguna relación más entre los números hexagonales y los que has obtenido anteriormente.

18. Pulsa . Ahora dispones de otro deslizador en la parte inferior de la ventana izquierda con el que puedes elegir el número de lados del polígono, de modo que combinando este deslizador con el que ya has utilizado antes puedes generar todos los números poligonales hasta el orden 12. Añade algunas columnas más en tu tabla para los números poligonales de orden 7, 8, ... Completa las nuevas columnas de la tabla ayudándote de los deslizadores.

19. Comprueba que la siguiente expresión algebraica te permite obtener cualquier número poligonal, en función de la longitud del lado n y del número de lados del polígono d: