|
|
Mecanismos que utilizan la combinación de dos
triángulos, uno con
un lado de longitud variable para transformar un
movimiento en otro. En muchos casos se trata de
convertir el movimiento de rotación de un punto
(manivela), en el deslizamiento de otro, que se traslada
según unas guías. Esta transformación se realiza con una
barra articulada en sus extremos (biela).
También tenemos ejemplos de la transformación de un
movimiento de rotación en otro movimiento también de
rotación en el mecanismo de disco acoplado de la
combinación de dos mecanismos de brazo oscilatorio en el
banco de carpintero.
|
|
|
6.1
|
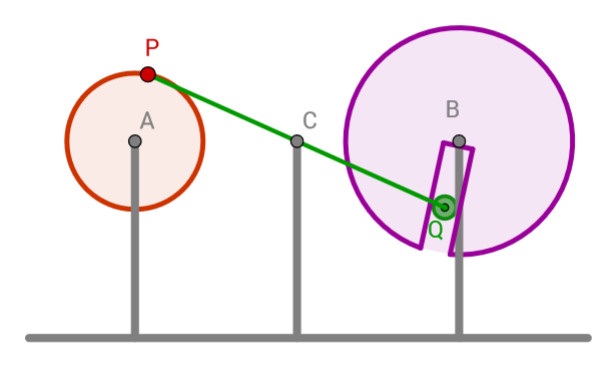
Combinamos dos triángulos, cada uno
con un lado de longitud variable. Transforma un
movimiento de rotación de un disco a otro disco.
|
Disco acoplado
|
|
ggb
|
|
6.2
|
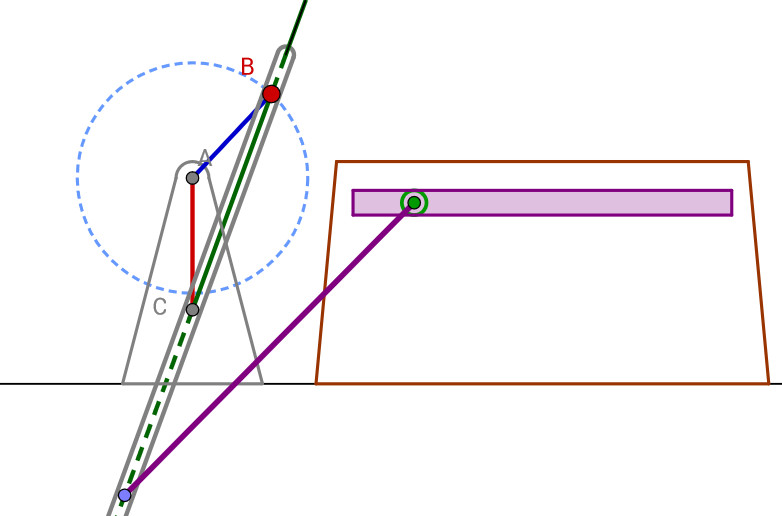
El primero actúa como un mecanismo
de brazo oscilatorio y transfiere su movimiento al
triángulo BDE, que tiene un funcionamiento parecido al
analizado en la máquina de vapor
|
Dos triángulos
|
|
ggb
|
|
6.3
|
El primer triángulo es un mecanismo
de brazo oscilatorio. El segundo triángulo con dos lados
de longitud variable
|
Corredera variable
|

|
ggb
|
|
6.4
|
Combinación de dos mecanismos de
brazo oscilatorio cuando se quiere una alimentación
lenta y retorno muy rápido. La barra se mueve con
velocidad casi constante de derecha a izquierda excepto
cuando B está justo arriba de A', que es cuando se
realiza el retorno.
|
Banco de carpintero
|

|
ggb
|
|
6.5
|
La manivela CD y la biela BC
imprimen movimiento arriba y abajo al balancín AE, que
con la biela EF transfiere el movimiento al pistón, que
se desplaza por el interior del cilindro
|
Balancín 1
|

|
ggb
|
|
6.6
|
Semejante al anterior, con los
elementos compuestos de otra manera. Ahora las bielas se
comunican por una barra que bascula.
|
Balancín 2
|

|
ggb
|
|
6.7
|
El mecanismo impulsor es la
manivela AB del triángulo ABC. La barra FJ actúa como
balancín alrededor de E y el triángulo EJL transmite el
movimiento al pistón en L
|
Motor de balancín
|

|
ggb
|
|
6.8
|
a manivela AB tiene recorrido sobre
un arco e impulsa el punto C en un movimiento de vaivén
lateral. El triángulo isósceles DCE, con DE variable,
consigue que el pistón haga dos ciclos completos, cada
vez que B recorre el arco en uno de los sentidos.
|
Motor de doble recorrido
|

|
ggb
|
|
6.9
|
Aplicación que relaciona los cuatro
triángulos estudiados: el gato elevador,la máquina de
vapor, el brazo oscilatorio y el cilindro hidráulico
|
Los cuatro
triángulos en una aplicación
|

|
ggb
|