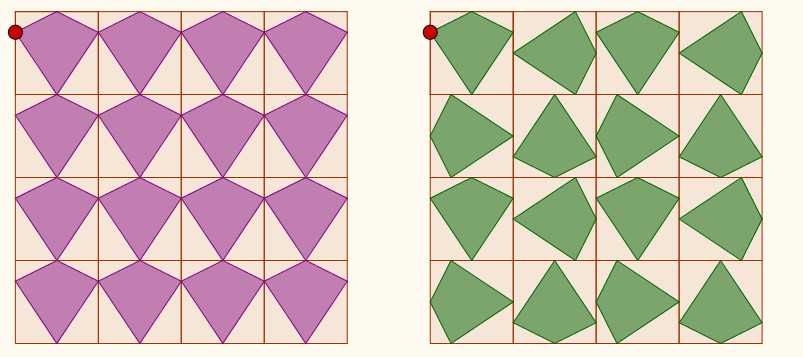
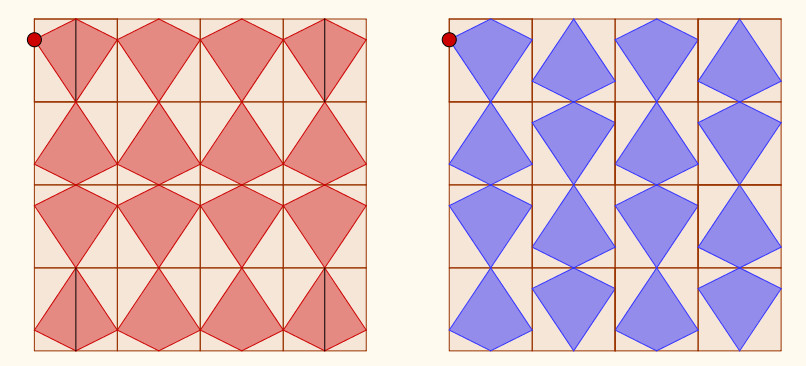
Los movimientos en el plano que mantienen las distancias, las isometrías, son la herramienta que permite pasar de unos azulejos a otros para construir un mosaico. Dedicamos un par de clases en la sala de Informática para trabajar los movimientos con GeoGebra y aplicarlos a alguna de las soluciones:

1. Traslación (con dos vectores situados sobre los lados del cuadrado),

2. Rotación de 90º (alrededor de uno de los vértices del cuadrado). Cuando tenemos una baldosa 2x2, la trasladamos con vectores sobre los lados de los cuadrados,

3. Simetría axial (respecto de los lados del cuadrado) y

4. Simetría central o rotación de 180º (alrededor del punto medio de los lados).

En cada uno de ellos nos paramos a ver los diferentes resultados que obtenemos para el mosaico. Aquí tenemos las composiciones con una de las cometas:

Movimientos plano

Intentamos que estas construcciones tengan un punto móvil (el que se ha marcado en rojo en los diseños) para que todos los polígonos se transformen de la misma forma que el inicial. GeoGebra permite activar la animación de ese punto para que se desplace sobre uno de los lados del cuadrado llevando todos los polígonos con él.
Una cuestión interesante a valorar con los alumnos es la forma de los huecos. Por las condiciones del problema tendremos que la mitad del mosaico es de color y la otra mitad -la formada por los “huecos” que deja nuestro diseño-, es blanca y compone nuevas formas que podemos analizar y, en algunos casos prever, mediante el estudio de la baldosa elegida junto con el movimiento utilizado.

Anterior                 Índice             Siguiente