Las simetrías en el cubo.

Estudiaremos los elementos de simetría del cubo y, a partir de ellos, buscaremos los de los otros cuatro sólidos platónicos.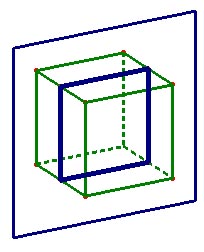

Para simplificar, un plano de simetría de un poliedro podría ser considerado como un espejo colocado en un corte del cubo, de forma que entre lo que queda del cubo y su imagen especular, podamos reconstruir el cubo completo.

Uno de los planos de simetría es paralelo a dos caras opuestas y corta al cubo por los puntos medios de las aristas. ¿Cuántos planos de simetría como éste cortan paralelos a dos caras?

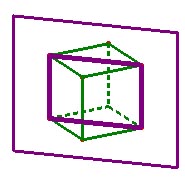Hay otro tipo de planos de simetría que cortan al cubo por las diagonales de las caras y por cada par de aristas opuestas. ¿Cuántos planos de simetría van por las diagonales?

Un eje de rotación es una recta que atraviesa el poliedro y que, si el cuerpo gira alrededor de ella, vuelve a coincidir consigo mismo antes de dar una vuelta completa. El orden de rotación de un eje es el número de veces que coincide el cuerpo consigo mismo hasta dar la vuelta completa.Por ejemplo este eje del cubo es de orden 4 porque cada giro de 90º hace que el cubo coincida con su posición inicial.

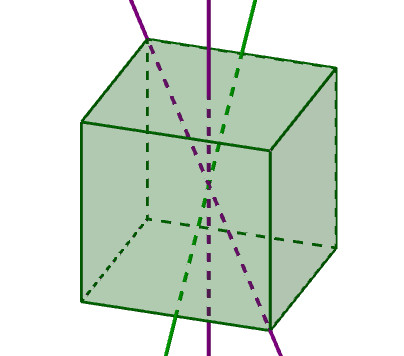Applet del cubo

Hay tres tipos de ejes de rotación: los tres que atraviesan el cubo por el centro de las caras, los cuatro que unen vértices opuestos por la diagonal espacial del cubo y los seis que pasan por los puntos medios de aristas opuestas y que son paralelos a las diagonales de las caras.

Una vez tenemos los elementos de simetría del cubo, el omnipoliedro puede ser de gran utilidad para encontrar los de los otros cuatro sólidos platónicos, los encajes de unos en otros tienen mucho que ver con los planos de simetría y ejes de rotación comunes.