|
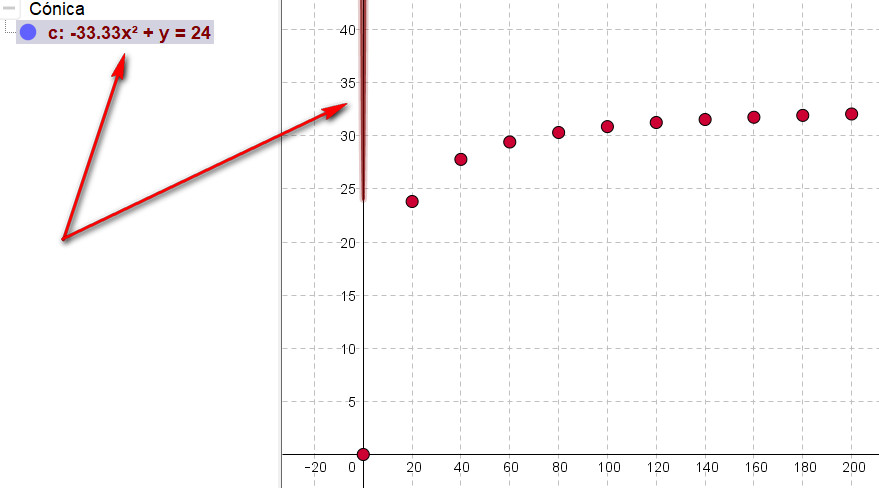
Lo que ocurre es que las graduaciones de los ejes no están preparadas para ese rango de valores. Es necesario “acomodar” los ejes a los valores que encontramos en la tabla -20<x<200, -5<y<40. Entre esos valores se ha construido la gráfica de la siguiente aplicación: |
|
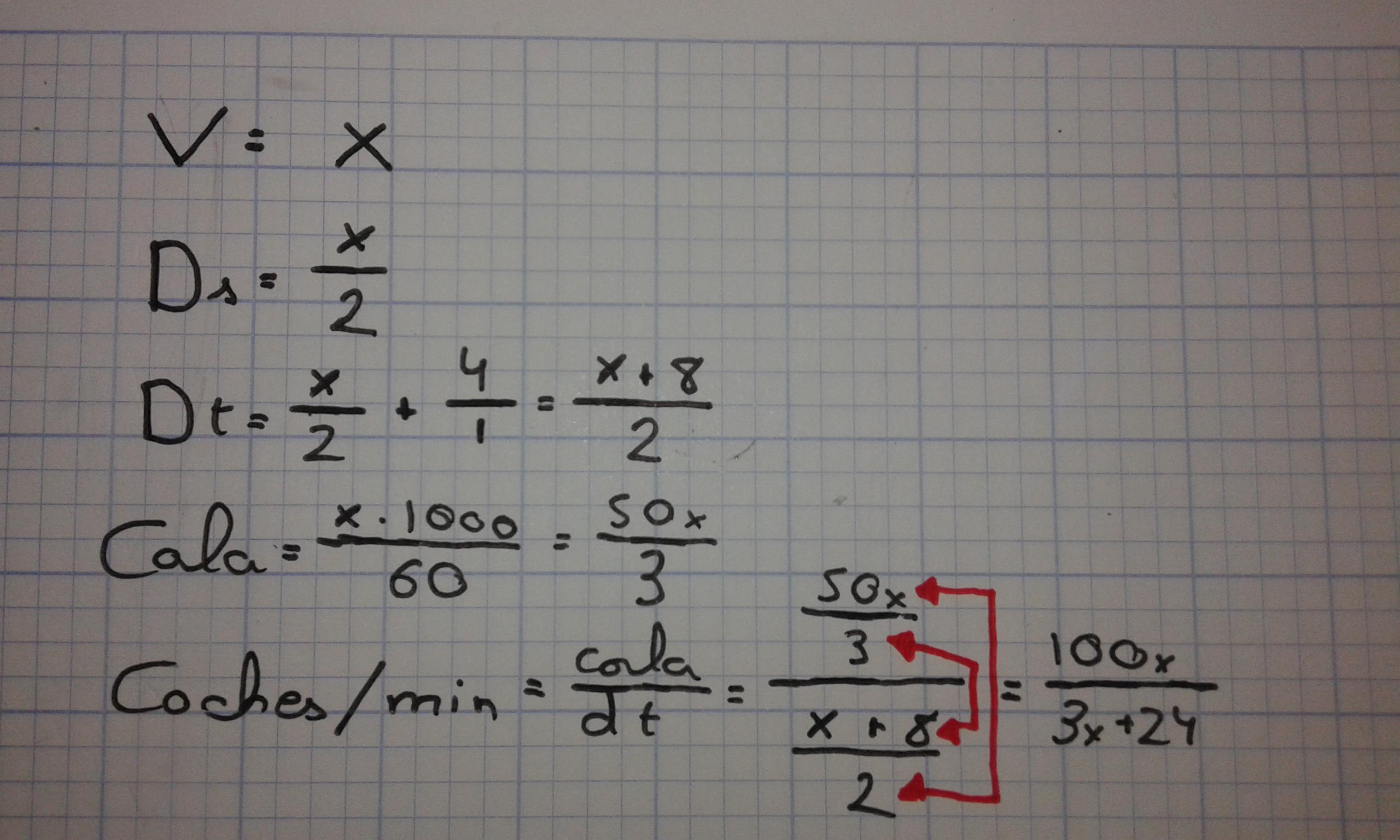
La gráfica que vemos no corresponde con la que esperábamos. En el debate inicial preveíamos encontrar el tráfico más fluido a una velocidad intermedia. Por ahora no solo no la hemos encontrado, sino que no parece que la vayamos a encontrar si las cosas siguen así. Profundizaremos en nuestro trabajo para comprender lo que está ocurriendo Ahora pasamos a la obtención de la fórmula que nos permita averiguar cuántos coches pasarán en un minuto cuando van a una velocidad x. Aquí tenemos la foto con móvil del trabajo de un alumno:
Representamos la gráfica sobre los puntos construidos anteriormente. Si se introduce la función en la barra de entrada de GeoGebra hay que tener en cuenta que solo se dispone de una sola línea. Coloca primero la fórmula sin paréntesis y=100x/3x+24. Se puede apreciar una línea roja en la parte superior del eje de ordenadas. Cuando ocurre un error de este tipo podemos aprovecharlo didácticamente: pedir acerquen el cursor a la línea que se ha dibujado y que analicen por qué GeoGebra nos dice que corresponde a una parábola, es más, si dejamos visible la ventana algebraica, nos dice que la expresión de esa curva es y=33.33x2+24. Coloca ahora la fórmula con paréntesis en la barra de entrada la fórmula y comprueba que pasa por los puntos. Este es un ejemplo que ilustra cómo el software invita a los alumnos a reflexionar sobre las consecuencias de sus errores y les proporciona ayudas para corregirlos por ellos mismos. El que la curva no pase por alguno de los puntos es útil para detectar un error, pero lo más importante es que ofrece la oportunidad al alumno de profundizar en su aprendizaje. El profesor puede orientar su trabajo para averiguar por qué ha ocurrido y qué debe hacer para resolverlo correctamente.
|
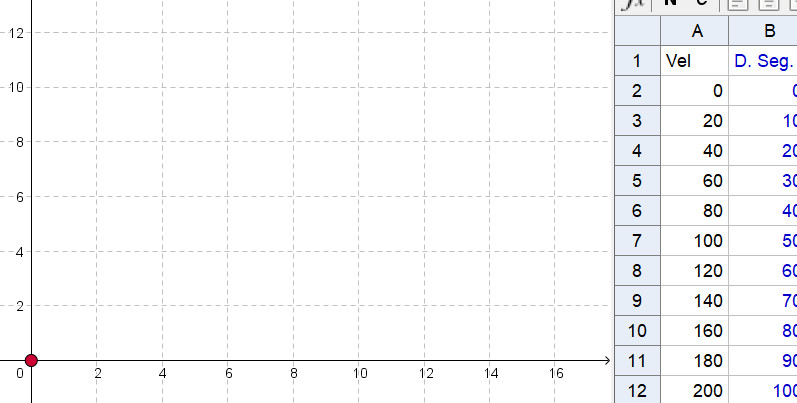 La columna de la derecha ya contiene los puntos que deben
aparecer en la ventana gráfica, pero al principio puede ocurrir
que no veamos más que un punto (0,0) en el origen de
coordenadas. Es el que nos dice que si los coches no se mueven,
no pasa ninguno por el punto fijado.
La columna de la derecha ya contiene los puntos que deben
aparecer en la ventana gráfica, pero al principio puede ocurrir
que no veamos más que un punto (0,0) en el origen de
coordenadas. Es el que nos dice que si los coches no se mueven,
no pasa ninguno por el punto fijado.