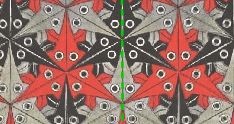
2.2. La Simetría axial.
Una figura tiene un eje de simetría cuando la podemos separar en dos partes exactamente iguales que admiten una de las siguientes pruebas:
-
Cada una de las mitades es la imagen especular de la otra mitad, es decir, si colocas un espejo en posición vertical al diseño sobre el eje, la figura que componen la mitad que queda visible y su imagen en el espejo conforman la figura original.
-
Podemos plegar el papel por el eje y las dos partes coinciden. Si damos un giro de 180º en el espacio alrededor de la recta, una de las dos mitades cae exactamente sobre la otra mitad.
¿Por qué crees que algunas personas ven la simetría axial como un elemento de belleza de los objetos?
¿Recuerdas algún edificio de tu país que tenga simetría axial?
G4D, Creado con GeoGebra
Página anterior Volver al índice Página siguiente Mapa de la Web
![]()
![]()
![]()