|
2
|
M. C. Escher
|
|
|
|
|
2.1
|
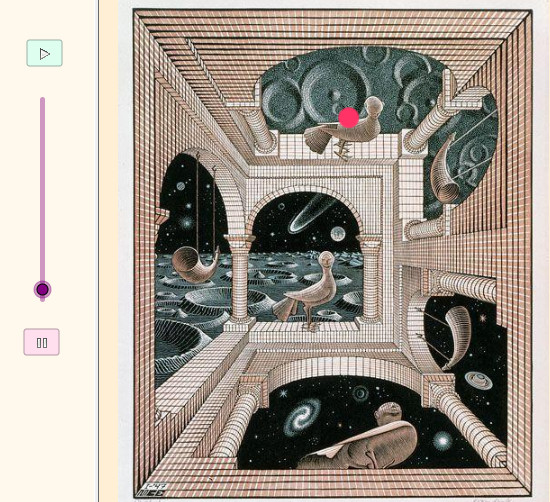
Seis
ventanas en las que cada suelo es techo de otro mundo.
Una bola cae desde cada techo hasta su suelo y busca un
nuevo techo para volver a caer |
Otro mundo II
|
|
ggb |
|
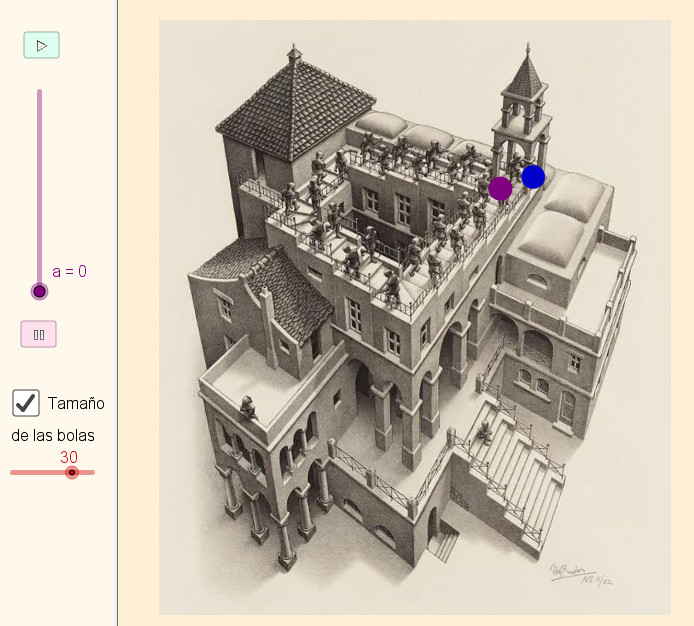
2.2
|
Introducimos unas pelotas de
color en las escaleras que siempre ascienden o
descienden, según se realice el recorrido en un sentido
o en otro |
Ascenso y descenso |
 |
ggb |
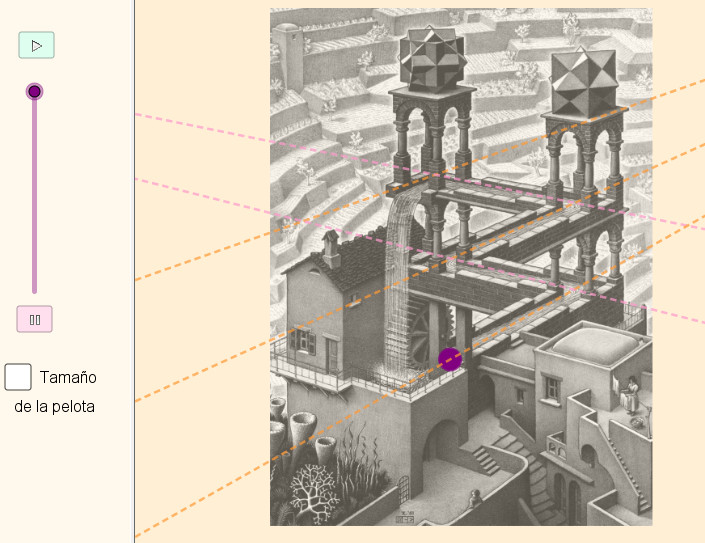
2.3 |
Una bola flota en el agua del
acueducto, se precipita por la cascada y vuelve al
principio |
Cascada |
 |
ggb |
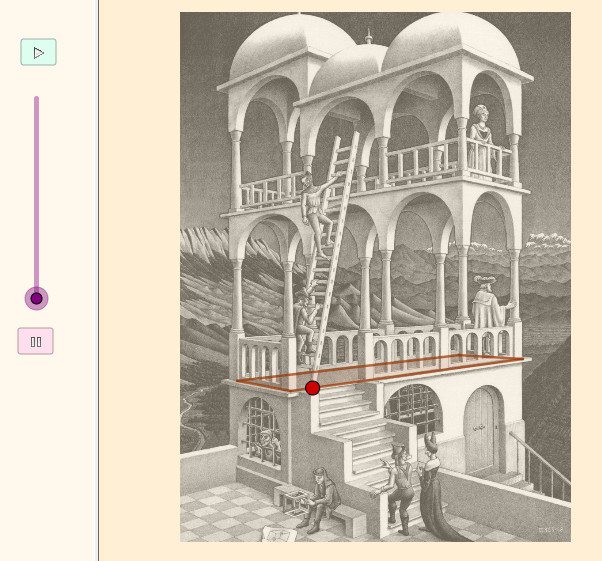
2.4 |
La bola hace un recorrido por
las plantas y el techo de la edificación hasta detenerse
en el cubo de Necker qu sostiene el personaje de la
parte inferior izquierda |
Bellvedere |
 |
ggb |
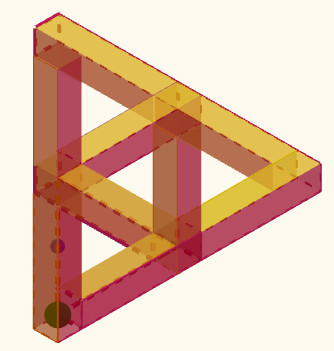
2.5 |
Dos animaciones sobre el triángulo imposible de R.
Penrose. En una se desvela la imposibilidad y en la otra
se confunde aún más nuestro cerebro con una pelota en su
interior |
Triángulo Imposible |
 |
ggb |
2.6 |
Tres mundos coexisten simultáneamente con terrazas
exteriores quenos introducen en el interior de un
edificio nos llevan a situaciones contradictorias |
Relatividad |
 |
ggb |
2.6 |
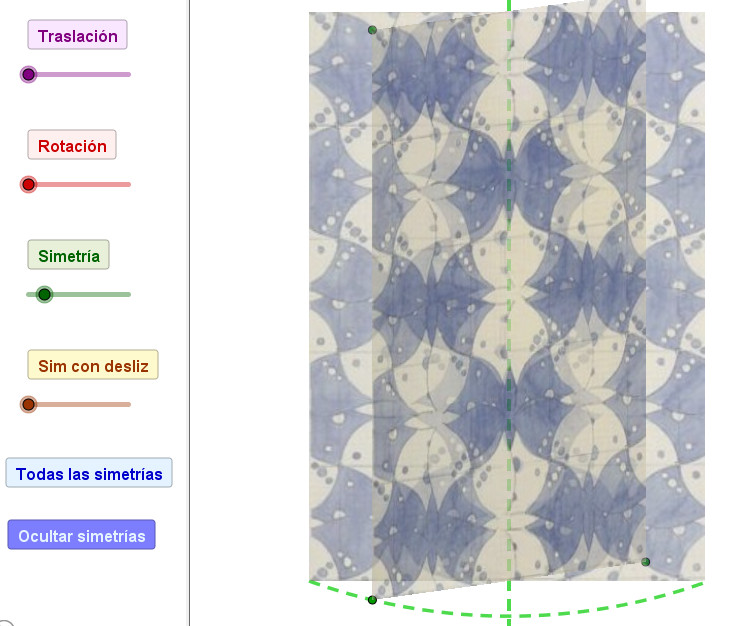
Construcción con un aparente eje de simetría axial en el
que reina la confusión: dentro-fuera, arriba-abajo,
interior-exterior, suelo-techo. Nada es lo que parece |
Concavidad y
convexidad |
 |
ggb |