| p1 | pg | pm | cm | p2 | pgg | pmg | pmm | cmm | p3 | p3m1 | p31m | p4 | p4m | p4g | p6 | p6m |
4.4.12.a. Mosaico Escher 123. Peces voladores. Grupo p31m.
G4D, Creado con GeoGebra
Elementos de simetría.
El esquema de elementos de simetría se parece mucho al anterior (p3m1): tiene los mismos ejes de simetría y simetría con deslizamiento y también los vectores de traslación.
La diferencia la encontramos en la simetría rotacional: este grupo, además de tener centros de rotación de orden 3 en los vértices de los triángulos que forman los ejes de simetría, también los tiene en los centros de esos triángulos. Esto obliga a que las tres figuras del interior del triángulo tengan la misma forma.
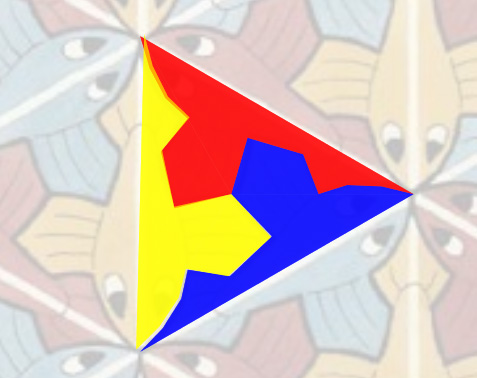
Baldosa poligonal.
Es un triángulo isósceles que se obtiene al tomar uno de los
triángulos de la trama de ejes de simetría y unir su centro con dos vértices. En
este caso, su interior se divide en tres partes iguales (según un centro de
rotación de orden 3), cada una de esas tres piezas es la mitad de uno de los peces
voladores.



Construcción del mosaico.
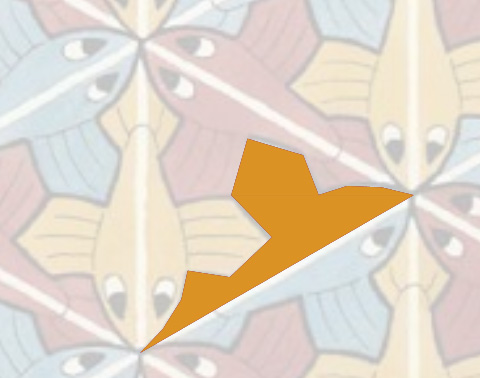
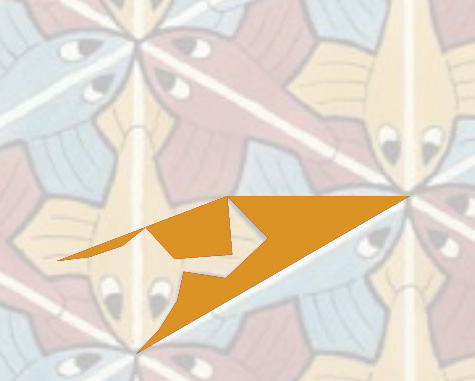
El primer paso es construir las tres mitades de los peces a partir de una de ellas utilizando el centro de rotación. Después componemos los tres peces voladores completos mediante las simetrías axiales respecto de los ejes que pasan por los lados del triángulo.
En el siguiente se utilizan dos vectores de traslación independientes para formar dos nuevos grupos de tres peces.
Si llevamos manualmente el deslizador verde a la parte superior, aparece otro nuevo de color azul junto al anterior con el objetivo de . Se señala con un círculo uno de los grupos de tres peces voladores y su simétrico respecto de una de las rectas coloreadas de amarillo.
Este mosaico incorpora un segundo deslizador que sólo aparece cuando el verde está en la parte superior para mostrar el efecto de la simetría con deslizamiento en este mosaico. Es conveniente parar la animación con el icono de la esquina inferior izquierda y llevar el punto verde manualmente hacia arriba. Aparece un nuevo deslizador azul, para ver cómo uno de los grupos de peces voladores realiza primero una simetría axial y acaba con un deslizamiento hasta llegar a su posición en el mosaico.
Página anterior Volver al índice Página siguiente Mapa de la Web
![]()
![]()
![]()